Сумма внутренних углов любого выпуклого шестиугольника является постоянной величиной и может быть вычислена по общей формуле для многоугольников. Это важное геометрическое свойство находит применение в различных областях математики и инженерии.
Содержание
Формула расчета суммы углов
Для любого выпуклого n-угольника сумма внутренних углов вычисляется по формуле:
S = (n - 2) × 180°
Где n - количество сторон (углов) многоугольника. Для шестиугольника (n = 6):
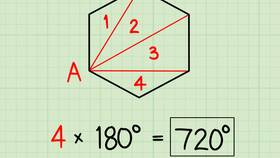
S = (6 - 2) × 180° = 4 × 180° = 720°
Доказательство формулы
Формула выводится следующим образом:
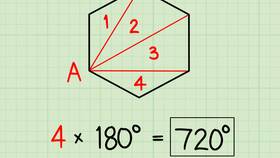
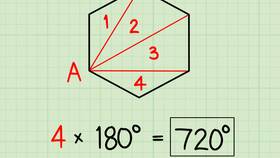
- Любой n-угольник можно разбить на (n - 2) треугольника
- Сумма углов каждого треугольника равна 180°
- Общая сумма углов равна количеству треугольников, умноженному на 180°
- Для шестиугольника получаем 4 треугольника × 180° = 720°
Свойства углов правильного шестиугольника
В правильном (равностороннем и равноугольном) шестиугольнике:
| Характеристика | Значение |
| Сумма всех внутренних углов | 720° |
| Величина одного внутреннего угла | 120° (720° ÷ 6) |
| Сумма внешних углов | 360° (как у любого выпуклого многоугольника) |
| Величина одного внешнего угла | 60° (360° ÷ 6) |
Практическое применение
Знание суммы углов шестиугольника используется в:
- Архитектуре и строительстве
- Проектировании сотоподобных структур
- Компьютерной графике и 3D-моделировании
- Геодезии и картографии
- Дизайне и декоративном искусстве
Особенности невыпуклых шестиугольников
Для невыпуклых (вогнутых) шестиугольников:
- Сумма внутренних углов также равна 720°
- Один или несколько внутренних углов превышают 180°
- Формула (n - 2) × 180° остается справедливой
- Разбиение на треугольники требует особого подхода
Таким образом, сумма внутренних углов любого шестиугольника - как выпуклого, так и невыпуклого - всегда составляет 720 градусов.