Описанный четырехугольник (также называемый тангенциальным) - это четырехугольник, в который можно вписать окружность. Для таких фигур существует важное свойство, касающееся суммы длин их сторон.
Содержание
Основное свойство описанного четырехугольника
В любом описанном около окружности четырехугольнике суммы длин противоположных сторон равны между собой:
| AB + CD | = | BC + AD |
где AB, BC, CD, AD - длины сторон четырехугольника.
Доказательство свойства
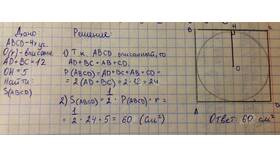
- Пусть в четырехугольник ABCD вписана окружность
- Точки касания делят стороны на отрезки: AB = a + b, BC = b + c, CD = c + d, DA = d + a
- Складываем противоположные стороны: AB + CD = a + b + c + d
- BC + AD = b + c + d + a
- Получаем равенство AB + CD = BC + AD
Практическое применение
- Проверка возможности вписать окружность в четырехугольник
- Решение геометрических задач на вычисление сторон
- Построение описанных четырехугольников по заданным параметрам
Примеры расчетов
| Четырехугольник | Стороны | Сумма противоположных сторон |
| Ромб | a, a, a, a | a + a = a + a |
| Дельтоид | a, a, b, b | a + b = a + b |
| Пример 1 | 5, 7, 6, 4 | 5 + 6 = 7 + 4 (11=11) |
Важное следствие
Полупериметр описанного четырехугольника равен сумме длин любых двух соседних сторон, образующих пару с общей точкой касания вписанной окружности.