Сумма внутренних углов любого четырехугольника является постоянной величиной и не зависит от его формы и размеров. Это фундаментальное свойство евклидовой геометрии.
Содержание
Основная теорема о сумме углов четырехугольника
Для любого выпуклого четырехугольника сумма внутренних углов равна 360 градусам. Это можно выразить формулой:
∠A + ∠B + ∠C + ∠D = 360°
Доказательство теоремы
Способ 1: Разбиение на треугольники
- Проводим диагональ в четырехугольнике, разделяя его на два треугольника
- Сумма углов каждого треугольника равна 180°
- Общая сумма углов двух треугольников: 180° × 2 = 360°
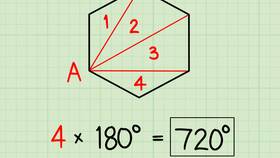
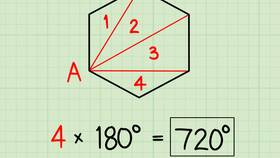
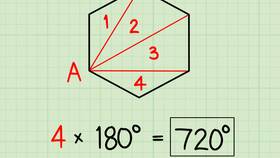
Способ 2: Использование формулы суммы углов n-угольника
Общая формула суммы внутренних углов выпуклого n-угольника:
S = (n - 2) × 180°
Для четырехугольника (n=4):
S = (4 - 2) × 180° = 2 × 180° = 360°
Примеры расчетов
| Тип четырехугольника | Сумма углов |
| Прямоугольник | 90° + 90° + 90° + 90° = 360° |
| Ромб | 60° + 120° + 60° + 120° = 360° |
| Произвольный четырехугольник | 80° + 100° + 70° + 110° = 360° |
Особые случаи
Вогнутые четырехугольники
Для вогнутых четырехугольников сумма углов также равна 360°, хотя один из углов будет больше 180° (вогнутый угол).
Самопересекающиеся четырехугольники
Для самопересекающихся четырехугольников (например, "бантика") сумма углов может отличаться от 360°.
Практическое применение
- Проверка правильности построения четырехугольников
- Решение геометрических задач на вычисление неизвестных углов
- Конструирование и инженерные расчеты
- Компьютерная графика и 3D-моделирование
Пример задачи
В четырехугольнике ABCD известны три угла: ∠A = 85°, ∠B = 110°, ∠C = 70°. Найдите угол D.
Решение:
∠D = 360° - (85° + 110° + 70°) = 360° - 265° = 95°
Вывод
Знание того, что сумма углов четырехугольника равна 360 градусам, является важным инструментом в геометрии и находит применение во многих практических областях. Это свойство остается верным для любых выпуклых и вогнутых четырехугольников в евклидовом пространстве.