Сумма внутренних углов пятиугольника - это важная геометрическая характеристика, которая определяется количеством его сторон. Пятиугольник (пентагон) представляет собой многоугольник с пятью углами и пятью сторонами.
Содержание
Формула расчета суммы углов
Для любого выпуклого n-угольника сумма внутренних углов вычисляется по формуле:
S = (n - 2) × 180°
где n - количество сторон многоугольника.
Расчет для пятиугольника
| Количество сторон (n) | Формула | Расчет | Результат |
| 5 | (5 - 2) × 180° | 3 × 180° | 540° |
Доказательство формулы
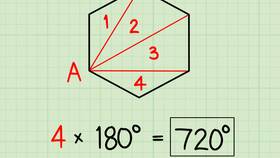
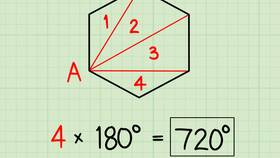
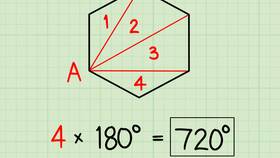
Формула основывается на разбиении многоугольника на треугольники:
- Из одной вершины проводим диагонали ко всем несмежным вершинам
- Пятиугольник разбивается на 3 треугольника (n - 2 = 5 - 2 = 3)
- Сумма углов каждого треугольника равна 180°
- Общая сумма: 3 × 180° = 540°
Примеры пятиугольников
| Тип пятиугольника | Особенности углов |
| Правильный пятиугольник | Все углы равны 108° (540° ÷ 5) |
| Неправильный пятиугольник | Углы различны, но сумма 540° |
| Выпуклый пятиугольник | Все углы меньше 180°, сумма 540° |
| Вогнутый пятиугольник | Один угол больше 180°, сумма 540° |
Практическое применение
Знание суммы углов пятиугольника используется в:
- Архитектуре и строительстве
- Проектировании технических деталей
- Компьютерной графике и 3D-моделировании
- Геодезических измерениях
Проверка расчета
Для правильного пятиугольника можно проверить расчет:
- Каждый угол правильного пятиугольника: 108°
- Сумма 5 углов: 5 × 108° = 540°
- Результат совпадает с расчетом по формуле
Заключение
Сумма внутренних углов любого пятиугольника всегда равна 540 градусов, независимо от его формы и размеров, при условии что он является простым (несамопересекающимся) многоугольником. Это свойство вытекает из общей формулы для суммы углов n-угольника и подтверждается геометрическими построениями.