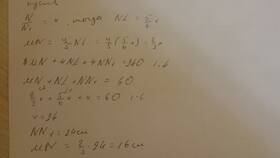Параллелепипед - это объемная геометрическая фигура, у которой все грани являются параллелограммами. Чтобы вычислить сумму длин всех его ребер, необходимо знать основные параметры этой фигуры.
Содержание
Свойства параллелепипеда
- Имеет 12 ребер
- Все ребра разделяются на 3 группы по 4 параллельных ребра
- В прямоугольном параллелепипеде все углы прямые
- Ребра можно разделить на длину (a), ширину (b) и высоту (c)
Формула суммы длин ребер
Сумма длин всех ребер параллелепипеда вычисляется по формуле:
L = 4 × (a + b + c)
где:
a - длина
b - ширина
c - высота параллелепипеда
Примеры расчетов
| Размеры (см) | Расчет | Сумма ребер (см) |
| a=2, b=3, c=4 | 4 × (2 + 3 + 4) | 36 |
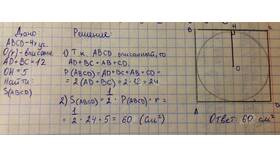
| a=5, b=5, c=5 (куб) | 4 × (5 + 5 + 5) | 60 |
| a=1.5, b=2, c=3.5 | 4 × (1.5 + 2 + 3.5) | 28 |
Частные случаи
Куб (частный случай параллелепипеда)
У куба все ребра равны (a = b = c), поэтому формула упрощается:
L = 12 × a
Прямоугольный параллелепипед
Формула остается стандартной, но все углы между ребрами составляют 90°
Практическое применение
Знание суммы длин ребер параллелепипеда полезно для:
- Расчета материала для каркаса конструкции
- Определения длины окантовочных элементов
- Решение задач по геометрии
- Проектирования упаковки
Дополнительные сведения
Для вычисления суммы ребер необходимо:
- Измерить три различных измерения параллелепипеда
- Убедиться, что все измерения выражены в одинаковых единицах
- Правильно применить формулу, учитывая количество ребер
Геометрическое обоснование
Формула 4×(a+b+c) объясняется тем, что:
- параллелепипед имеет по 4 ребра каждого размера
- все измерения (длина, ширина, высота) встречаются в четырех экземплярах
- поэтому сумму всех ребер можно представить как учет каждого измерения четырежды